原文:http://fatelei.github.io/2015/09/08/
按照指定的权重求随机数
描述:通常取随机数,取到每个数字的概率都是一样,比如取 n 次,取到某个数的概率都是 1/n。现在情况发生了变化,要随机取的数,每个数字都被设置了一个权值(weight),比如:
上面这个图表的含义是:进行随机取数,取到 1 的概率是 1/5,取到 2 概率是 2/5,取到 3 的概率是 2/5。现在要求你使用代码完成这个按照不同权值进行取值的过程。
一开始想到方法是:
使用一个数组 value ,数组的下标对应于这个权重的范围,下标对应的值就是要求的值,比如还是上面这个例子,比如在 1 < x <= 3这个区间范围内,然后对整个区间长度求随机值,rand(1, 5) 会得到一个下标值,然后根据这个下标值去获取想要的值。这个解法的问题是,如果某个值的权值很大,那么需要一个很大的数组,这样会非常非常消耗内存,显然不是一个很好的解决方法。不过当时也没有想到更好的方法。
晚上回来想了想,有没有可以优化的方向
1 2 3 | p(x = 1) = 1/5 (x <= 1) p(x = 2) = 2/5 (1 < x <= 3) p(x = 3) = 2/5 (3 < x <= 5) |
转换成累积概率:
1 2 3 | cp(x = 1) = 1/5 (x <= 1) cp(x = 2) = 3/5 (1 < x <= 3) cp(x = 3) = 1 (3 < x <= 5) |
有上面这个映射关键,在 0 - 1 随机取一个数 x,如果 x <= cp[i] ,i 就是所要求的结果:
Python 实现
1 2 3 4 5 6 7 | import random def random_by_weight(values, cp): for v, w in zip(values, cp): rand = random.randint(0, 1) if rand <= w: return v |
选自:http://blog.csdn.net/v_july_v/article/details/6132775
3.1、选择算子
遗传算法使用选择运算对个体进行优胜劣汰操作。
适应度高的个体被遗传到下一代群体中的概率大;适应度低的个体,被遗传到下一代群体中的概率小。
选择操作的任务就是从父代群体中选取一些个体,遗传到下一代群体。
基本遗传算法(SGA)中选择算子采用轮盘赌选择方法。
Ok,下面就来看下这个轮盘赌的例子,这个例子通俗易懂,对理解选择算子帮助很大。
轮盘赌选择方法
轮盘赌选择又称比例选择算子,其基本思想是:各个个体被选中的概率与其适应度函数值大小成正比。设群体大小为N,个体xi 的适应度为 f(xi),则个体xi的选择概率为:

轮盘赌选择法可用如下过程模拟来实现:
(1)在[0, 1]内产生一个均匀分布的随机数r。(2)若r≤q1,则染色体x1被选中。(3)若qk-1<r≤qk(2≤k≤N), 则染色体xk被选中。 其中的qi称为染色体xi (i=1, 2, …, n)的积累概率, 其计算公式为:
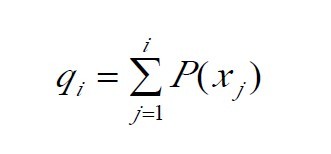
积累概率实例:

轮盘赌选择方法的实现步骤:
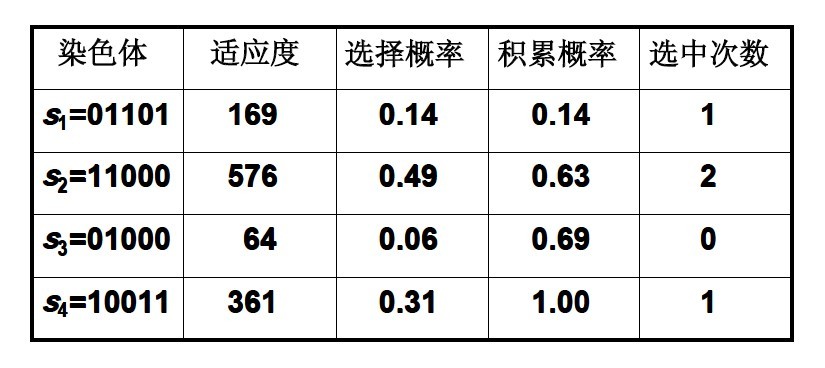
(1)计算群体中所有个体的适应度值;(2)计算每个个体的选择概率;(3)计算积累概率;(4)采用模拟赌盘操作(即生成0到1之间的随机数与每个个体遗传到下一代群体的概率进行匹配)来确定各个个体是否遗传到下一代群体中。例如,有染色体
s1= 13 (01101)s2= 24 (11000) s3= 8 (01000)s4= 19 (10011)假定适应度为f(s)=s^2 ,则
f (s1) = f(13) = 13^2 = 169f (s2) = f(24) = 24^2 = 576f (s3) = f(8) = 8^2 = 64f (s4) = f(19) = 19^2 = 361染色体的选择概率为:

染色体的累计概率为:

根据上面的式子,可得到:

例如设从区间[0, 1]中产生4个随机数:
r1 = 0.450126, r2 = 0.110347
r3 = 0.572496, r4 = 0.98503